
This post was originally published in 2019 with 9 different challenges. We have added an additional challenge and will present our results in more detail on March 17, 2021. Register for the webinar: https://qontigo.com/event/top-10-challenges-of-credit-construction/.
We have developed an algorithm to produce thousands of robust issuer-specific and generic rating/sector credit curves. In this blog post, we discuss the challenges associated with credit curve construction, and how we solved them, presented with illustrative interactive charts.
1. Lots of curves…
We begin with the scale of the problem: to support the full range of applications of credit curves we need to build lots of them. Rate and spread term structures are one of the cornerstones of fixed-income analysis and so there are many different applications: risk model construction, asset pricing, relative value analysis, liability discounting… the list goes on. To support these applications, we require broad issuer curve coverage, as well as broad coverage for sector or rating-based credit curves. In addition, these curves must be granular: full-term structures, with differentiation across currency, subordination tier, region, rating and industry. The challenge is to develop a fitting algorithm that can robustly calculate all these curves on a daily basis, and do so in reasonable time. The chart below summarizes the number of curves produced on a typical day for a selection of currencies. Cloud-based solutions such as Databricks are employed to facilitate quick calculation of all the curves – a full 19yr history of daily curves can be generated in a matter of days. The curve history is based on analytics of over 1 million instruments, which are also calculated using cloud technology.
Source: Qontigo
2. How is an issuer actually defined?
Before we embark on the construction of issuer spread curves, we must stop to think about what we mean by an issuer. This apparently trivial question is easy to overlook, but is absolutely fundamental to the construction of robust and meaningful issuer spread curves. To build an issuer curve we will group bonds that have exposure to the same underlying credit risk, and fit a curve through them (more on this bit later).
The hard part is determining which bonds have the same credit risk – corporate hierarchies are complex and bonds are issued at many different levels. To effectively group bonds for curve construction you must first group legal entities within a corporate hierarchy. These groupings are what we call Risk Entities: a group of legal entities that have the same credit risk exposure. This is challenging because there is often no definitive indicator that tells you how to group entities, and so you must rely on different sources of information including equity issuance, CDS issuance, guaranteed borrower information, ratings and market trading conventions such as tickers. To meet our range of uses these groupings should be dynamic to account for corporate actions, and cover in excess of 20,000 corporate hierarchies. Below we show a simplified General Electric hierarchy with the 3 Risk Entities identified.
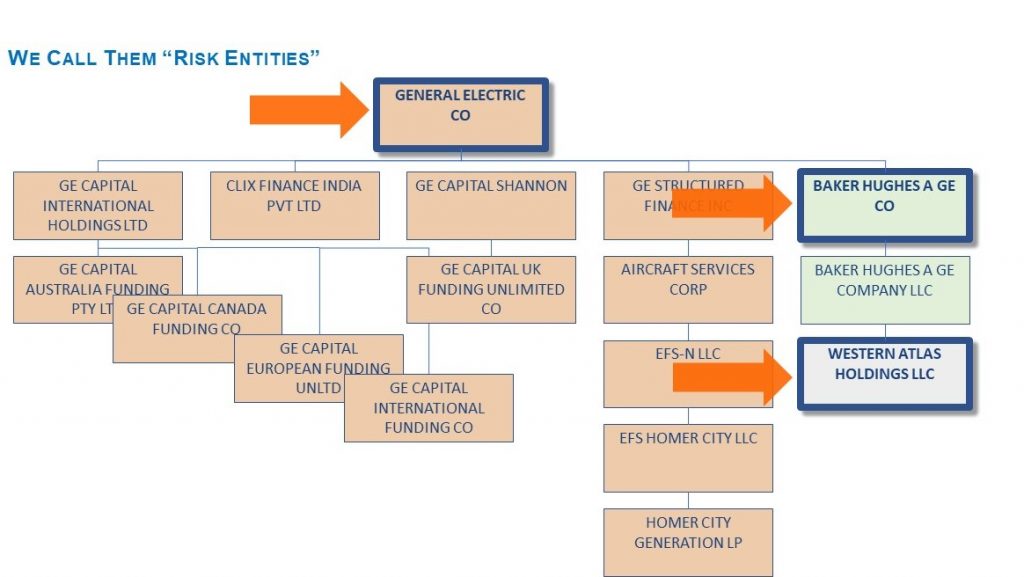
Source: Refinitiv, Qontigo
3. Dealing with stale or erroneous prices
Poor quality data is an unavoidable feature of fixed income. The challenge when building curves is to ensure that the curve construction algorithm is robust, and that means effective outlier detection and removal. The chart below shows an example curve where outlying bonds have been detected and down-weighted: data points that are hollower have less weight applied to them in the curve fitting algorithm.
Source: Qontigo
4. Granularity matters
Defining an issuer is one thing, but there can be many curves associated with it. Take a relatively large issuer like Lloyds Bank, shown below. Here we demonstrate the granularity in the currency of issuance and debt seniority dimensions. It’s clear that if we don’t capture this granularity we would mix issuer signal as the curve levels are significantly different.
Source: Qontigo
5. Accurate curves can still lead to noisy time series
It is not enough to fit the bonds accurately each day. Particularly for risk model applications, it’s important that the curve histories are also smooth through time. To support both pricing and risk applications there’s a need to strike a balance between pricing accuracy and time series volatility. We achieve this by employing a noise reduction algorithm that incorporates mean reversion to the level, but dampens jumps though time. An example is shown below for Autodesk Inc.; here missing and erroneous prices contribute noise to the issuer curve level, and the mean reverting smoothing dampens the noise without deviating too far from the level.
6. Rating transitions cause jumps in spreads
Rating-based curves e.g. AA-Financials, need to be carefully constructed to avoid sudden jumps in spread levels following upgrades or downgrades. A classic example is that of Greece, shown below. Here we compare a simple weighted average BBB sovereign spread (a spread average over all EUR BBB sovereign bonds) which suddenly drops in the level when Greece is downgraded. The Axioma curves shown in grey are robust to rating changes, as the full surface of ratings curves is fitted together rather than in isolation.
7. How can you fit a term structure with only one bond?
One general challenge with issuer curve construction is that you very quickly run into market thinness, or put another way, you find there aren’t many bonds to use to fit the curve. It turns out that this is the case most of the time. There are many curve fitting techniques out there, but most of the time they are applied to construction problems where there is lots of data e.g. the US Treasury curve, or the Goldman Sachs curve. What do we do about those issuers that have only a few bonds, or even just one bond? How can we fit a term structure? Answer: we use information from ‘comparables’, or peer issuers. The key idea is that we can reasonably infer a term structure shape from the term structure shapes of other issuers in the same or similar sectors, trading at similar spread levels. The chart below illustrates this for a North American issuer in the energy sector: Centennial Resource Development Inc. Although we only have one issuer bond, the upward sloping term structure is informed by other North American and global energy issuers trading at similar spread levels.
8. Trading accuracy of fit against smoothness
When fitting curves to bond prices or spreads one has to carefully consider the curve fitting technique to employ – exact fits (interpolation) can be applied to a small number of highly liquid instruments, or approximate fits (smoothing) can be applied to a larger set of noisy data. When building issuer credit curves smoothing approaches are typically applied. The chart below illustrates the idea: there are many bonds and peers (comparables) so an interpolation would lead to very oscillatory (and probably useless) spread curve. A smooth non-parametric form is used in this example, which strikes the right balance between smoothness and accuracy of fit. Care must also be taken with the extrapolation at each – we use an x-axis compression method which ensures a continuous gradient in the extrapolation region, and ensures that the extrapolation is not simply implied by the non-parametric function used to interpolate.
9. How can generic rating curves be constructed in thin markets?
When building generic rating/sector curves, whether or not a curve can be constructed depends on the amount of information. For example, let’s say we’re trying to build a BB2 curve for North American pharmaceutical issuers, issuing in USD. What if there aren’t any BB2 issuers? Similarly, how can we control the different rating curves with a sector to ensure that the AA2 curve is lower than the A2 i.e. a monotonicity constraint. To get around these issues related to market thinness one must calibrate all rating/sector curves together. An example is shown below where the 3-dimensional surface shows rating curves alongside the underlying bond issuance. The entire surface is fitted at once rather than each individual rating curve in isolation. This allows for rating granularity, and means the BB2 curve can be calculated by interpolation, even where no bonds exist! Fitting the surface also means we can control the monotonicity.
In addition, the shape of the surface is informed by issuers outside the cluster, meaning robust spread curves can be built for thin markets at the edges of the surface. As an example, the history of high yield Latin American Non-financial spread is shown below.
10. How can curve quality be assessed?
Even with advanced and robust algorithms there is still a significant chance that curves will not be suitable for all applications. Data errors and missing data can still lead to gaps and extreme spread levels. The challenge is to be able to identify poor quality curves out of the thousands that are generated each day, and to be able assess whether sudden moves are reasonable or not. An automated scoring mechanism known as SFEN (Stochastic Filter and Enhancer) is used to score all curves and identify those meeting quality thresholds for different applications.
SFEN works by comparing observed spread paths with paths from a tolerant stochastic model that is informed by three key properties of the observable time series:
- Stochastic volatility;
- Kurtosis (fat tails);
- Correlation with other spread time series identified as peers.
At each trade date, SFEN simulates thousands of model paths and a peer-informed path. Movements of each curve can be scored by measuring the distance between paths generated by SFEN and the observed paths. The chart below shows an example: the shaded area is the difference between the observed path and the peer-implied path over the period during which the observed spread lies outside of the projected model distribution. The larger the shaded area, the lower the score of the curve time series.
Source: Qontigo



